树状数组

树状数组其实是一种针对于前缀和的优化。

可以将区间查询和修改的复杂度讲从 $O(n)$ 降到 $O(\log n)$。

算法主要思路

正常的前缀和数组如果显示为一个树的话是这样的：

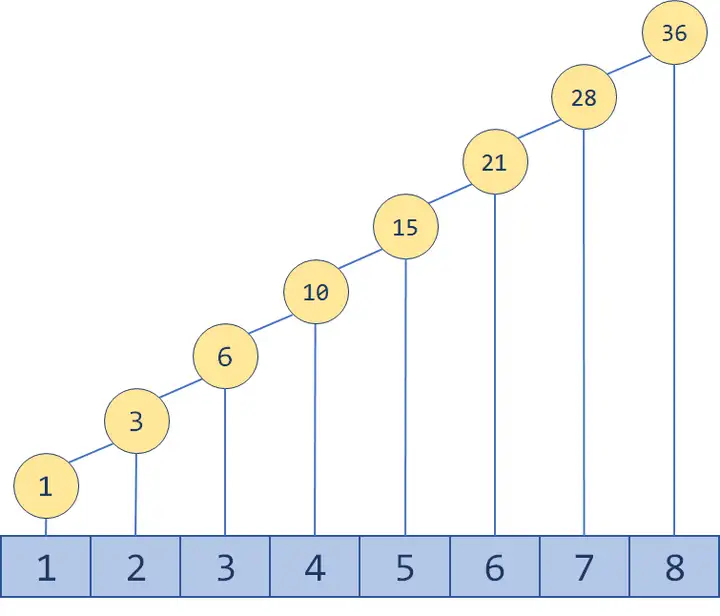
也就是 $f_i$ 维护的区间是 $[1, i]$。

但是在树状数组中，$f_i$ 不用维护那么多，只有维护 $(i – \text{lowbit}(i), i]$：

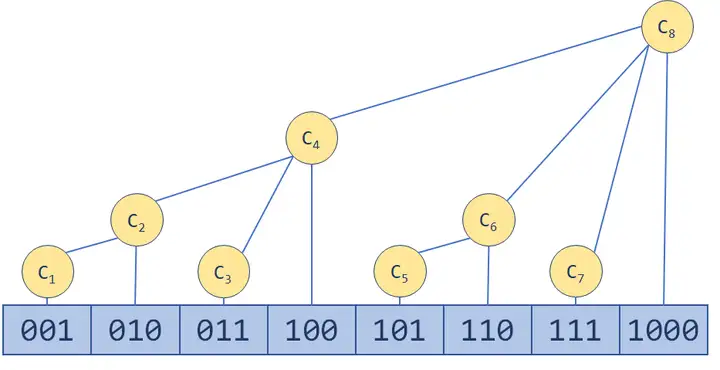
更新：从初始节点开始，每次更新现在的节点的编号加上 $\text{lowbit}(i)$，直到达到 $n$。

比如我们想更新 $3$ 号节点，我们可以先更新 $3$ 号，再更新 $4$ 号，最后更新 $8$ 号，这样就全部更新完了。

这样用树状数组只用更新 $3$ 次，而普通线段树需要更新 $6$ 次。

虽然小的数据看不出太大的差别，但是如果是大数据，那么差别就大了。

统计：从初始节点开始，每次节点编号减去 $\text{lowbit}(x)$，直到到达 $1$。

模板题：P3374 【模板】树状数组 1 – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

代码：

#include <bits/stdc++.h>

using namespace std;
/*
*/
#define int long long
int s[1000005], a[1000005], n, m;
#define lowbit(x) ((x) & (-x))
void update(int i, int x) {
    for (int j = i; j <= n; j += lowbit(j)) {
        s[j] += x;
    }
}
int q(int n) {
    int ans = 0;
    for (int i = n; i > 0; i -= lowbit(i)) {
        ans += s[i];
    }
    return ans;
}
int query(int l, int r) {
    return q(r) - q(l - 1);
}
signed main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> n >> m;
    m = 1;
    for (int  i = 1; i <= n; i ++) {
        cin >> a[i];
        update(i, a[i]);
    }
    while (m --) {
        int o; cin >> o;
        int l, r; cin >> l >> r;
        if (o == 1) update(l, r);
        else cout << query(l, r) << "\n";
    }
    return 0;
}