线段树

线段树，运用了分治的方法，将一个数组拆成了一堆区间。

线段树和普通的树的区别在于普通的树是维护数，而线段树是维护区间。

我们一般用数组表示法实现二叉树。

见图：

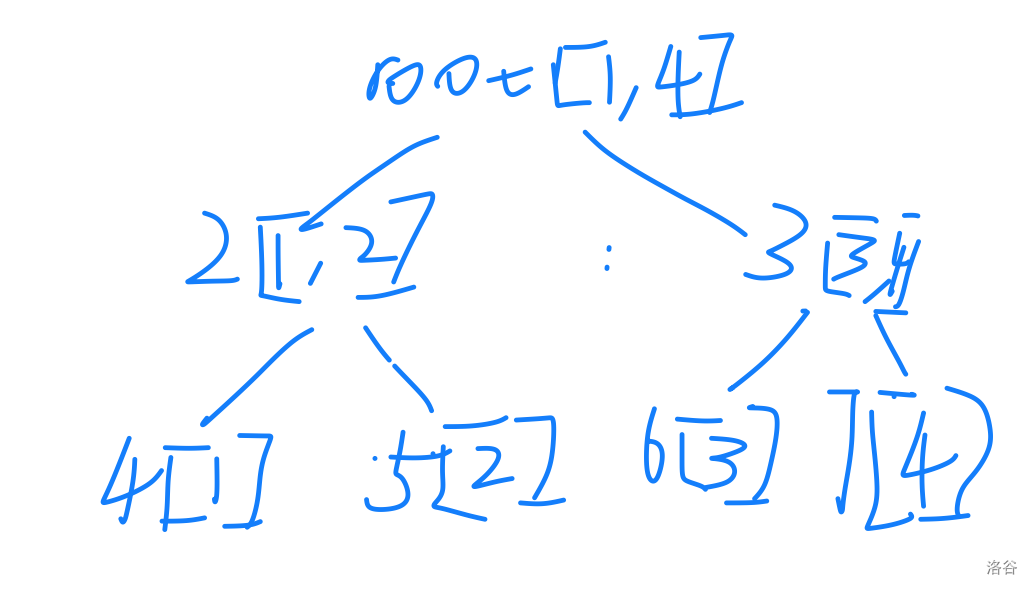
建树

首先，我们从根开始递归，如果当前节点是叶子节点，那么让这个节点等于 $l$，否则递归左右子树，然后更新节点。

pushdown

这个操作是线段树的精华。

这个操作意在维护懒标记并下传标记至子树。

1. 把标记传到子树。
2. 通过标记乘长度对子树的值进行操作。
3. 清空标记。

区间修改

主要思路就是找到目标区间进行操作。

我们定义 $x$ 为需要加的数。

从根节点进行递归，如果目前的区间和目标区间完全没有相交的地方，直接返回。

如果存在包含关系，那么直接加上维护的区间长度乘 $x$，因为我们需要把区间的每个数都加 $x$。

如果相交，但是不包含，那么我们先 pushdown，然后把目前区间拆分成两个继续往子树去寻找。

最后更新节点。

区间查询

基本上就和修改一样。

区间查询在查询到目标区间后不是修改，而是直接返回数据。

代码

/*

 problem :
 by : ztrztr(luogu 602124)
 date : 2022/10/16
 update : 2022/10/16

*/
#include <bits/stdc++.h>
using namespace std;
#define int long long
int seg[1000005], n, mark[1000005], a[1000005];
namespace fun{
    void pd(int nw, int len) {
        mark[nw * 2] += mark[nw];
        mark[nw * 2 + 1] += mark[nw];
        //Update mark.
        seg[nw * 2] += mark[nw] * (len - len / 2);
        seg[nw * 2 + 1] += mark[nw] * (len / 2);
        //Update SegTree.
        mark[nw] = 0;
        //Free mark.
    }
    void build(int nw, int l, int r) {
        if (l == r) {
            seg[nw] = a[l];
            //Leaf node.
//          cout << "[Debug] Finded leaf node " << nw << "\n";
            return; 
        }
        int mid = (l + r) / 2;
//        cout << "11\n";
        build(nw * 2, l, mid);
        build(nw * 2 + 1, mid + 1, r);
        seg[nw] = seg[nw * 2] + seg[nw * 2 + 1];
        //update
    }
    void update(int l, int r, int nw, int x, int nl, int nr) {
        if (nl > r || nr < l) return;
        if (nl >= l && nr <= r) {
            seg[nw] += (nr - nl + 1) * x;
            if (nr > nl) mark[nw] += x;
            return;
        }
        pd(nw, nr - nl + 1);
        update(l, r, nw * 2, x, nl, (nl + nr) / 2);
        update(l, r, nw * 2 + 1, x, (nl + nr) / 2 + 1, nr);
        seg[nw] = seg[nw * 2] + seg[nw * 2 + 1];
        //update
    }
    int find(int l, int r, int nw, int nl, int nr) {
        if (nl > r || nr < l) return 0;
        if (nl >= l && nr <= r) return seg[nw];
        pd(nw, nr - nl + 1);
        int leftAns = find(l, r, nw * 2, nl, (nl + nr) / 2);
        int rightAns = find(l, r, nw * 2 + 1, (nl + nr) / 2 + 1, nr);
        return leftAns + rightAns;
    }
}
using namespace fun;
namespace OI{
    void run() {
        int m;
        cin >> n >> m;
        for (int i = 1; i <= n; i ++) cin >> a[i];
        build(1, 1, n);
//      cout << "[Debug] Build OK!\n";
        while (m --) {
            int op; cin >> op;
            if (op == 1) {
                int x, y, z; cin >> x >> y >> z;
                update(x, y, 1, z, 1, n);
            } else {
                int x, y; cin >> x >> y;
                cout << find(x, y, 1, 1, n) << "\n";
            }
        }
    }
}
signed main() {
    ios::sync_with_stdio(false);
    OI::run();
    return 0;
}