搜索 & 图的储存和最短路算法

搜索

DFS

这种方法可以概括为：不撞南墙不回头，回过头来继续撞。

DFS，深度优先搜索，顾名思义就是每次递归到最深，然后回溯。

我们一般用递归函数实现 DFS。

例题：

用 DFS 求最短路：

#include <bits/stdc++.h>

using namespace std;
/*
*/
vector <int> e[100005], v[100005];
int n, m, vis[100005], s, t, ans = 0x7fffffff;
void DFS(int nw, int sum) {
    if (nw > n) return;
    if (nw == t) {
        ans = min(ans, sum);
        vis[nw] = 0;
        return;
    }
    for (int i = 0; i < e[nw].size(); i ++) {
        if (vis[e[nw][i]] == 0) vis[e[nw][i]] = 1, DFS(e[nw][i], sum + v[nw][i]);
    }
}
int main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> n >> m >> s >> t;
    for (int i = 1; i <= m; i ++) {
        int x, y, z; cin >> x >> y >> z;
        e[x].push_back(y);
        v[x].push_back(z);
    }
    DFS(s, 0);
    cout << ans;
    return 0;
}

BFS

这种方法可以概括为：如果我一层没扫完，我不会到下一层，只会把下一层的数据记住！

BFS，广度优先搜索（也叫宽度优先搜索），思路大概就是搜索到哪个点就把那个点的所有可以去的点入队，一直搜索直到到终点或者队列为空。

B3625 迷宫寻路 – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include <bits/stdc++.h>

using namespace std;
/*
bfs 学习
*/
int n, m, vis[1005][1005];
char a[1005][1005];
struct node{
    int x, y;
};
int main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) cin >> a[i][j];
    }
    queue <node> q;
    q.push((node){1, 1});
    while (q.size()) {
        int i, j;
        i = q.front().x;
        j = q.front().y;
        q.pop();
        if (vis[i][j]) continue;
        vis[i][j] = 1;
        if (i >= 1 && i <= n && j >= 1 && j <= m && a[i + 1][j] == '.') q.push((node){i + 1, j});
        if (i >= 1 && i <= n && j >= 1 && j <= m && a[i][j + 1] == '.') q.push((node){i, j + 1});
        if (i >= 1 && i <= n && j >= 1 && j <= m && a[i - 1][j] == '.') q.push((node){i - 1, j});
        if (i >= 1 && i <= n && j >= 1 && j <= m && a[i][j - 1] == '.') q.push((node){i, j - 1});
        if (i == n && j == m) {
            cout << "Yes";
            return 0;
        }
    }
    cout << "No";
    return 0;
}

图的储存

图论的基础，就是要存图。

图的主流储存有以下几种：

方式	优点	缺点
邻接矩阵	编写方便，遍历方便	容易 `MLE`
邻接表	遍历方便	…
链式向前星	内存使用量小	遍历有点复杂

综上所说，我还是推荐大家用邻接表，除非在特别卡空间的题目才用链式前向星。

邻接矩阵

顾名思义，邻接矩阵就是一个矩阵 ~(￣▽￣)~*

这个邻接矩阵的矩阵 $a_{i, j}$ 表示 $i \to j$ 这条边的权值，如果边不存在，则为 INF，如果 $i = j$，为 $0$。

现在我们看一道题目：

给定一个有向无环图，输出这个有向无环图的邻接矩阵，注意如果 $i = j$，$a_{i, j} = 0$。

第一行 $n$ 和 $m$，其中 $n$ 为顶点数，$m$ 为边数；第二行到第 $m + 1$ 行，为从顶点 $i$ 到顶点 $j$ 之间的边，$i$ 和 $j$ 之间以空格分隔。输入数据保证没有重边。

数据：

这个样例对应的图片：

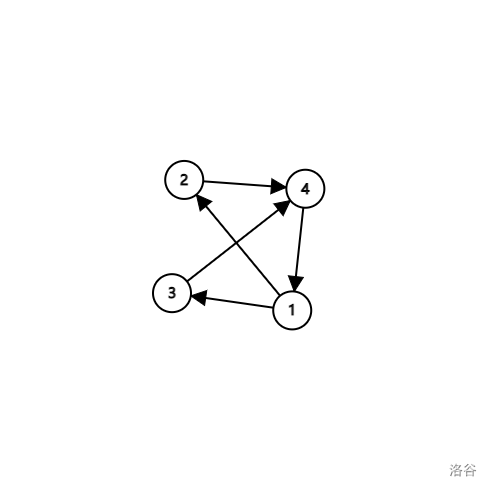
解题步骤：
首先我们要建图：

int n, m; cin >> n >> m;
for (int i = 1; i <= m; i ++) {
    int x, y; cin >> x >> y;
    a[x][y] = 1;//建立 x 到 y 的一条边
}

接下来就是输出，直接输出矩阵就行了，完整代码：

#include <bits/stdc++.h>
using namespace std;
int a[10005][2005];
int main() {
    int n, m; cin >> n >> m;
    for (int i = 1; i <= m; i ++) {
        int x, y; cin >> x >> y;
        a[x][y] = 1;
    }
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= n; j ++) {
            cout << a[i][j] << " ";
        }
        cout << "\n";
    }
    return 0;
}

然后我们试着提交一下，AC！！

邻接表

邻接表类似邻接矩阵，但是不会花费空间出储存不存在的边。

每个点都会有一个对应的 vector，这个点的所有能到达的点都会被 push_back 到 vector 里面，从而节省很多空间。

继续看一道题：

输入一个有向图（结点数小于 $100000$，边数少于 $200000$）。并打印该有向图的邻接表。

第一行 $n$ 和 $m$，其中 $n$ 为顶点数，$m$ 为边数；第 $2$ 行到第 $m + 1$ 行，为从顶点 $i$ 到顶点 $j$ 之间的边，$i$ 和 $j$ 之间以空格分隔。输入保证所有边 $(i,j)$ 的终点 $j$ 是单调不降的。输入不保证没有重边。

输出为起点结点编号:所有边终点结点编号。起点结点编号升序，终点节点编号按降序排列。

这道题的邻接表示意图如下：

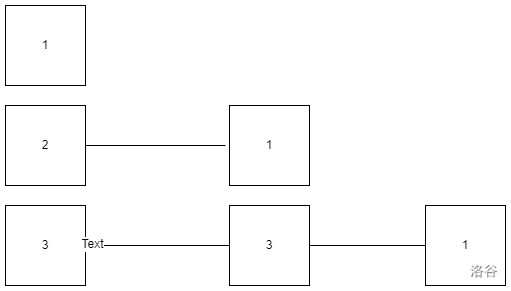
首先，我们先读入和建图：

for (int i = 1; i <= m; i ++) {
    int x, y; cin >> x >> y;//输入，建立一条从 x 到 y 的边。
    w[x].push_back(y);//点 x 多加一条通往 y 的边。
}

接着，输出,AC代码：

#include <bits/stdc++.h>
using namespace std;
vector <int> w[100005];
int main() {
    int n, m; cin >> n >> m;
    for (int i = 1; i <= m; i ++) {
        int x, y; cin >> x >> y;
        w[x].push_back(y);
    }
    for (int i = 1; i <= n; i ++) {
        cout << i << ":";
        for (int j = w[i].size() - 1; j >= 0; j --) {
            cout << w[i][j] << " ";
        }
        cout << "\n";
    }
    return 0;
}

链式向前星

这时一个占用空间最小的算法，原理就是把邻接表的 vector 换成链表，具体代码就不在这里展示了，有兴趣的同学可以看这个。

最短路

在生活中，我们经常用高德导航（或者百度），我们发现导航每次都可以找到最快的路线，为我们节省时间。这就是运用了求最短路的算法。

Floyd

在数据范围小的情况下，我们可以才用这个方法。

Floyd 是思维难度最低的最短路方法，思路是：

对于任何两点：$i$ 和 $j$，如果存在一个点 $k$ 使得 $\text{dis}{i, j} > \text{dis}{i, k} + \text{dis}{k, j}$，那么我们让 $\text{dis}{i, j} = \text{dis}{i, k} + \text{dis}{k, j}$。我们称这种操作为松弛操作。

我们遍历所有的 $i, j, k$（注意 $k$ 的循环时第一层），对 $\text{dis}{i, j}$ 进行松弛操作。

如果遍历完，那么 $\text{dis}$ 数组肯定是最短的了。

这种方法的时间复杂度是 $O(n^3)$，所有请务必要注意数据范围。

题目：P2888 [USACO07NOV] Cow Hurdles S

#include <bits/stdc++.h>

using namespace std;
/*
*/
int n, m, dp[1005][1005], M;
int main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> n >> m >> M;
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= n; j ++) {
            dp[i][j] = 0x7fffffff;
        }
    }
    //init
    for (int i = 1; i <= m; i ++) {
        int x, y, z; cin >> x >> y >> z;
        dp[x][y] = z;
    }
    //input
    for (int k = 1; k <= n; k ++) {
        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= n; j ++) {
                dp[i][j] = min(max(dp[i][k], dp[k][j]), dp[i][j]);
                //dp
                //floyd
            }
        }
    }
    while (M --) {
        int x; int y; cin >> x >> y;
        if (dp[x][y] == 0x7fffffff) cout << "-1\n";
        else cout << dp[x][y] << "\n";
    }
    //output
    return 0;
}

Dijkstra

这个算法基于贪心策略。

在这个算法中，图中的点被分为了两个集合：已扩展和未扩展。

我们定义 $d_i$ 为已扩展点到所有点的最小距离。

我们先从随便一个点出发（通常是 $1$ 号点），这时 $d_i$ 为和点 $1$ 连接的那些边。

我们每次选取一个最小的边，不断的扩展，直到全部扩展完，那么 $d$ 数组就是我们想要的了。

这个算法和 Prim 类似。

Dijkstra 堆优化

这个算法其实就是优先队列优化的 BFS。

思路：

第一步将起点入队。

用循环遍历所有和这个点有边的点。

如果这个点可以被松弛，那么松弛这个点，并将这个点入队

一直重复第二步到第三步，直到队列为空。

输出。

#include <bits/stdc++.h>

using namespace std;
/*
*/
vector <int> w[100005], v[100005];
int n, m, s, dis[100005];
bool vis[100005];
struct node {
    int d, p;
    const bool operator <(const node &x) const{
        return x.d < d;
    }
};
priority_queue <node> q;
int main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> n >> m >> s;
    for (int i = 1; i <= m; i ++) {
        int x, y, z; cin >> x >> y >> z;
        w[x].push_back(y);
        v[x].push_back(z);
    }
    for(int i = 1; i <= n; i ++) dis[i] = 0x7fffffff;//
    dis[s] = 0;//
    q.push((node){0, s});
    while (!q.empty()) {
        int nd, np;
        nd = q.top().d;
        np = q.top().p;
        q.pop();
        if (vis[np]) continue;
        vis[np] = 1;
        for (int i = 0; i < w[np].size(); i ++) {
            int nxt = w[np][i];
            if (dis[nxt] > dis[np] + v[np][i]) {//
                dis[nxt] = dis[np] + v[np][i];
                if (vis[nxt] == 0) q.push((node){dis[nxt], nxt});//
            }
        }
    }
    //BFS
    for (int i = 1; i <= n; i ++) {
        cout << dis[i] << " ";
    }
    return 0;
}

下一篇，树和森林。

一	二	三	四	五	六	日
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30

ztrztr

一名学生，喜爱 OI 与 Dev，文化课和 OI 都烂的一坨。

搜索

DFS

BFS

图的储存

邻接矩阵

邻接表

链式向前星

最短路

Floyd

Dijkstra

Dijkstra 堆优化

发送评论编辑评论

搜索

DFS

BFS

图的储存

邻接矩阵

邻接表

链式向前星

最短路

Floyd

Dijkstra

Dijkstra 堆优化

发送评论 编辑评论

推荐文章

发送评论编辑评论